Skip to content
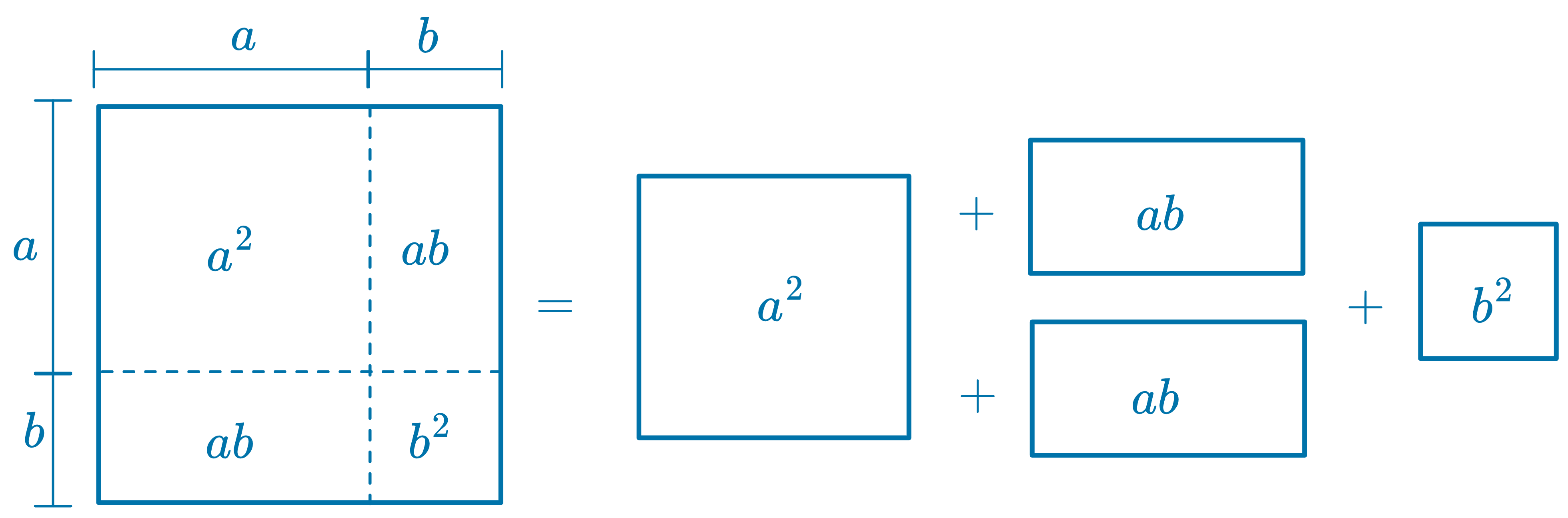
(a±b)2=a2±2ab+b2
Important:
(a−b)2=(b−a)2
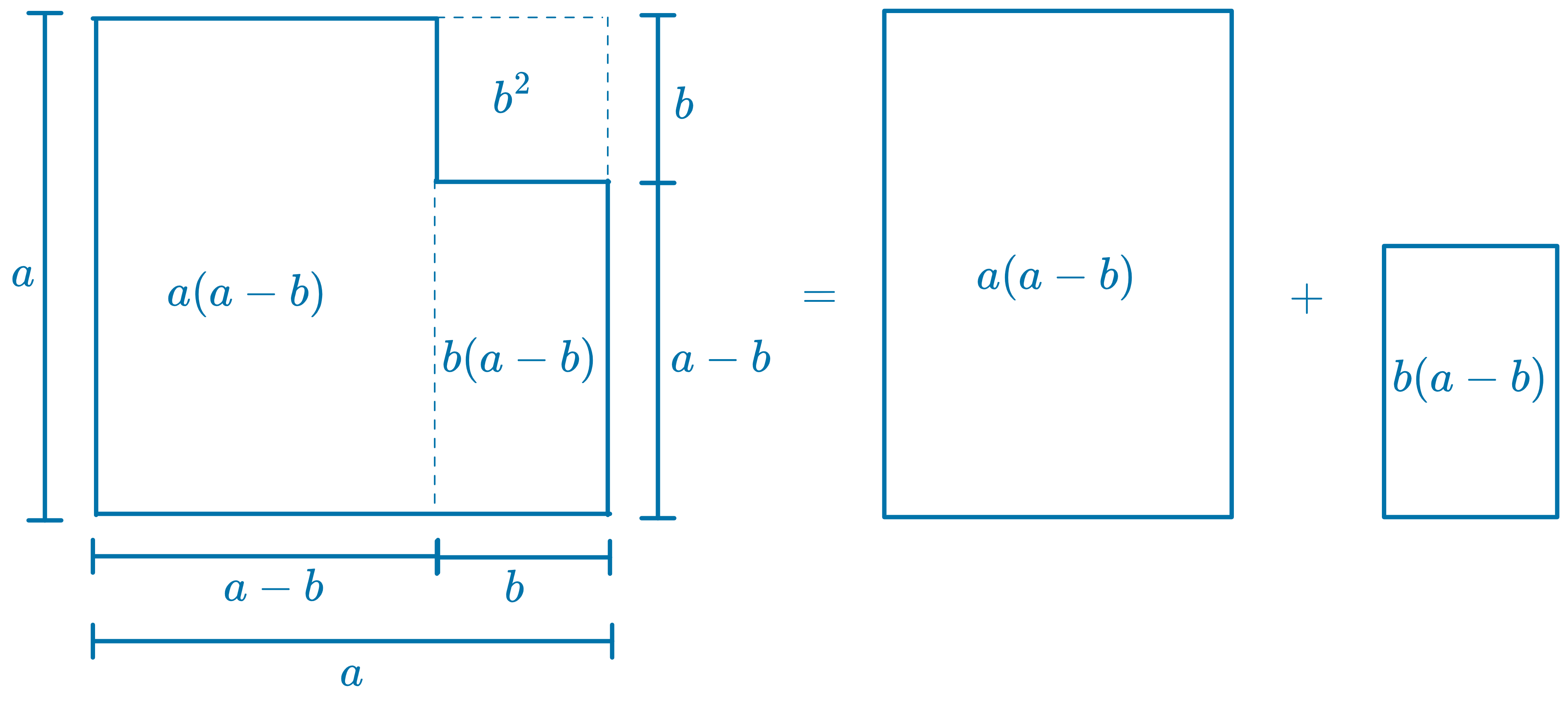
a2−b2=(a+b)(a−b)
a3+b3=(a+b)(a2−ab+b2)
a3−b3=(a−b)(a2+ab+b2)
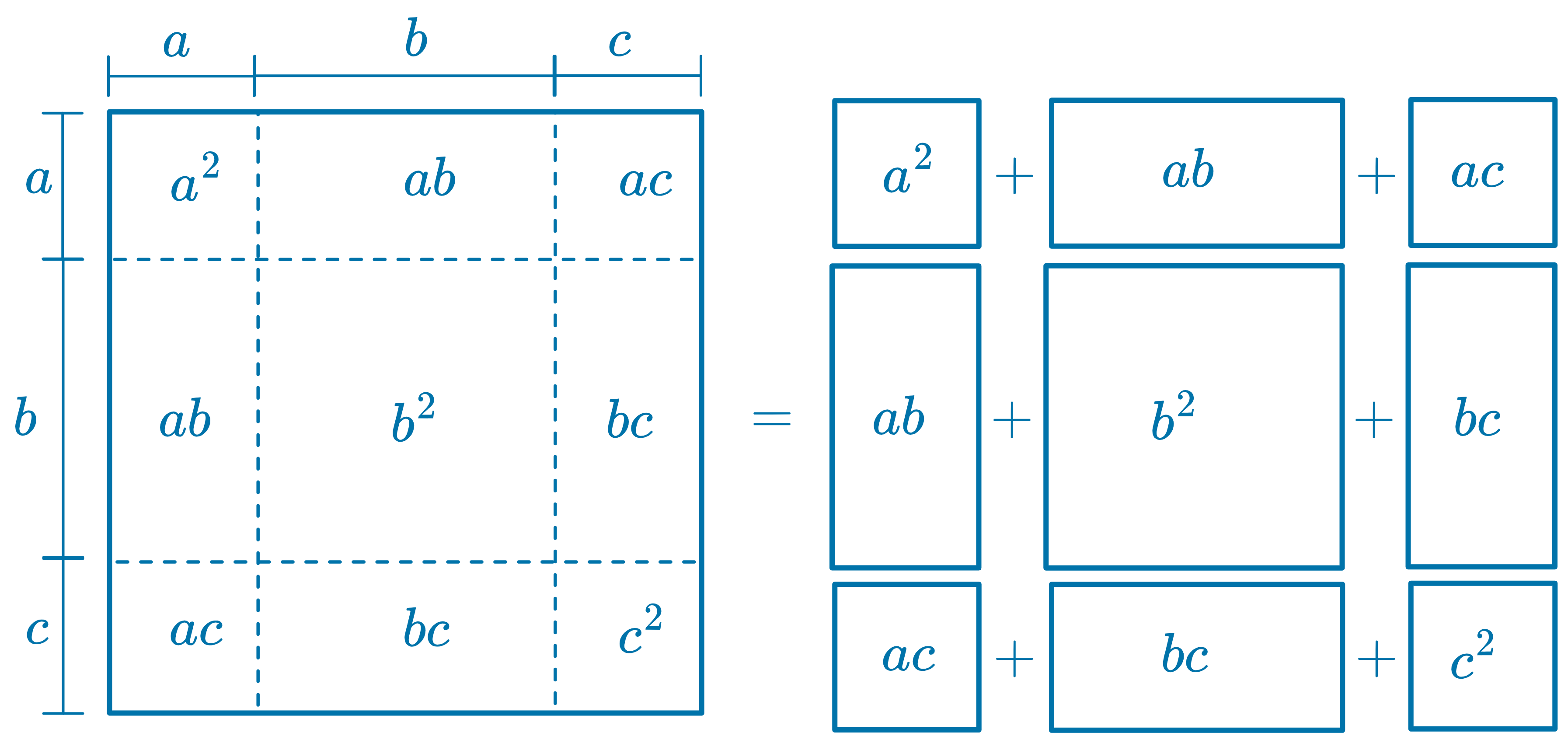
(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
Also:
(a+b−c)2=a2+b2+c2+2ab−2ac−2bc
(a−b+c)2=a2+b2+c2−2ab+2ac−2bc
(a−b−c)2=a2+b2+c2−2ab−2ac+2bc
(a−b−c)2=(−(b+c−a))2=(b+c−a)2
(a+b)3=a3+3a2b+3ab2+b3
(a−b)3=a3−3a2b+3ab2−b3
Also:
(a+b)3=a3+b3+3ab(a+b)
(a−b)3=a3−b3−3ab(a−b)
(a+b+c)3=a3+b3+c3+3(a+b)(b+c)(c+a)
Another form:
(a+b+c)3=a3+b3+c3+3a2(b+c)+3b2(a+c)+3c2(a+b)+6abc
Also:
(a+b+c)3=a3+b3+c3+3(a+b)(b+c)(c+a)−3abc
(x+a)(x+b)=x2+(a+b)x+ab
(x+a)(x+b)(x+c)=x3+(a+b+c)x2+(ab+bc+ac)x+abc
(a+b)2+(a−b)2=2(a2+b2)
(a+b)2−(a−b)2=4ab
(a+b)3+(a−b)3=2a(a2+3b2)
(a+b)3−(a−b)3=2b(3a2+b2)
(a+b)4−(a−b)4=8ab(a2+b2)
(x2+x+1)(x2−x+1)=x4+x2+1
(x2+xy+y2)(x2−xy+y2)=x4+x2y2+y4
In General:
(x2m+xmyn+y2n)(x2m−xmyn+y2n)=x4m+x2my2n+y4n
(a2+b2)(x2+y2)=(ax+by)2+(ay−bx)2
(a2+b2+c2)(x2+y2+z2)=(ax+by+cz)2+(ay−bx)2+(az−cx)2
a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−ac−bc)
a3+b3+c3=21(a+b+c)[(a−b)2+(a−c)2+(b−c)2]
a2+b2+c2−ab−ac−bc=21[(a−b)2+(a−c)2+(b−c)2]
(a+b+c)3−a3−b3−c3=3(a+b)(b+c)(c+a)
(a+b)(b+c)(a+c)+abc=(a+b+c)(ab+ac+bc)
(a−b)2+(b−c)2+(a−c)2=(a2+b2+c2)−2(ab+ac+bc)
- If a+b+c=0, then:
a2+b2+c2=−2(ab+ac+bc)
a3+b3+c3=3abc
a4+b4+c4=2(a2b2+a2c2+b2c2)
a5+b5+c5=−5abc(ab+ac+bc)
(ab+ac+bc)2=a2b2+a2c2+b2c2
- If ba+ab=2, then:
a=b
- If a2+b2+c2=ab+ac+bc, then:
a=b=c
- If a3+b3+c3=3abc and a+b+c=0, then:
a=b=c=0
- If a2+b2+c2+⋯+z2=0, then:
a=b=c=⋯=z=0
- If na+nb+⋯+nz=0, then:
a=b=⋯=z=0
- If x+x−1=a, then:
x2+x−2=a2−2
x3+x−3=a3−3a
x4+x−4=(a2−2)2−2